I am a political scientist who studies war, nuclear proliferation, and terrorism (mostly) using formal models. Currently, I am an associate professor in the University of Pittsburgh’s Department of Political Science. Before that, I was a Stanton Nuclear Security Postdoctoral Fellow at Stanford’s Center for International Security and Cooperation. I received a PhD from the University of Rochester in 2015.
If you want to know more, you can check my CV page.
Posted in Uncategorized
US and Iran diplomatic teams negotiating the nuclear deal’s implementation in 2016
Recently, some commentators have suggested that the Biden administration use Trump’s withdrawal from the Joint Comprehensive Plan of Action—the Iran Deal—as leverage to obtain a better agreement. This logic has a tempting appeal. If the United States appears to be less interested in an agreement, and Iran still wants one, then Iran might have to offer more concessions to coax the United States.
However, setting this as the expectation misses the bigger picture. The United States is in a poor bargaining position for three reasons. Negotiations like these are generally difficult for the opponent of the potential nuclear weapons state. Leaving the deal has caused Iran to become more capable of developing nuclear weapons, not less. And because the United States has shown a willingness to leave agreements, the United States must sweeten the pot to coax moderates in Iran to take a domestic political risk by entering a new deal.
As such, the Biden administration ought to temper expectations heading into the new round of negotiations.
Nuclear Negotiations Favor the Would-Be Proliferator
The first problem is structural. Nonproliferators—the United States in this case—generally have the inferior position.
The deadlock with Iran will end in one of three ways: Iran developing a nuclear weapon, preventive war, or a deal. The United States has a long-standing policy to curb nuclear proliferation worldwide. Iran—a long time adversary—does not get a pass here. So the first option is off the table.
Preventive war is not a good outcome either. Optimists may look at how Israel handled Iraqi and Syrian programs and aspire to replicate those precision strikes. But there are major differences between those programs and Iran’s. Iran is in later stages, with multiple key facilities. Anticipating potential strikes, Iran even built its Fordow facility underground. This would mean that an effective preventive war would require boots on the ground and a more expansive mission. Lessons from Afghanistan and Iraq indicate that the United States should think twice here.
The Fordow Fuel Enrichment Plant, most of which is underground
That leaves a deal as the final remaining option. As I write about in Bargaining over the Bomb, if the United States wants long-term Iranian compliance, the deal must be generous. That is because the agreement must be better for Iran than building a weapon. A starting point for negotiations is therefore to treat a potential proliferator as though it already has nuclear weapons. Put bluntly, the United States needs to afford Iran about the same amount of begrudging respect it gives to other nuclear powers, like Pakistan.
Yes, this is a high price to pay. But insufficient concessions will induce Iran to build nuclear weapons. At that point, the United States will have to give that begrudging respect anyway and suffer the systemic instability that comes with another nuclear power born into the world.
Iran’s Increased Nuclear Competency
One benefit of reaching an agreement is that Iran does not spend money and resources on building and maintaining nuclear weapons. As a result, the United States can somewhat tilt the agreement in its favor.
But this reveals the second problem with trying to obtain a better deal than what original Iran Deal provided. The United States withdrew from the agreement in 2018. Iran initially maintained compliance with provisions to freeze its nuclear infrastructure despite the Trump administration’s departure.
However, Iran recently reinitiated work on uranium centrifuges, the critical technology necessary to produce fissile material for nuclear power plants—and nuclear weapons. That means Iran can more easily build nuclear weapons today than it could four years ago.
If you want to stop someone from doing something, you will have to pay them more as doing that thing becomes cheaper and easier. That is Bargaining 101. But that means the United States must be more generous this time around, not less.
Furthermore, if the United States wastes time holding out for a better deal, Iran’s competency will only increase in the interim. That further shrinks the amount that negotiators can extract out of Iran.
The Inconsistency Premium
The final problem is signaling an unwillingness to stick to an agreement is actively harmful, not helpful.
Biden may want to reach an agreement now and stick to it in the long term, but Iran must worry about what will happen in 2024 or 2028. Will a Trump-thinking candidate come into office and tear up the agreement once again?
The fact that the United States did this once suggests that it could easily happen again. If so, why would a moderate in Iran want to expend domestic political capital that will not provide lasting benefits?
Fortunately, the United States can overcome this problem in the short-term. But that means sweetening the pot for moderates in Iran to go along with it and expose themselves to those political risks.
There Is Still Time
Fortunately, there are concrete steps the Biden administration can take to overcome these problems. Iran’s nuclear fate has not been sealed. What the United States does in the upcoming months may very well decide it.
The first step is to revert back to Obama era policies. This means terminating the Trump administration’s latest economic sanctions against Iran. The same goes for the targeted sanctions against Mohammad Javad Zarif, Iran’s Foreign Minister and chief negotiator of the Joint Comprehensive Plan of Action.
Mohammad Javad Zarif, shaking hands with U.S. lead negotiator John Kerry, in 2015
The second step is a change in rhetoric. This is a central policy goal for Iran, and obtaining it would reduce the payoff a nuclear weapon would provide. But right now, the United States is working against that. The two rivals are currently engaged in a stare down, waiting for the other side to blink to restart negotiations. For the reasons described above, Washington’s position gets worse as time progresses. Extending the invitation simultaneously softens the rhetoric and gets the process moving.
That is not to say that any of this will be politically easy. The original Iran Deal faced a fair degree of skepticism in Congress in 2015. More recently, some Republicans pushed Trump to send the Iran Deal to the Senate—precisely so that it can meet a public defeat.
In general, though, Americans should temper expectations. They currently have a bad hand and can only play the cards they currently have. It would be a mistake to let the misplaced hope of a perfect deal get in the way of a good deal.
Posted in Bargaining, nuclear weapons, Political Science, Preventive War, War
Tagged Fordow, Iran, John Kerry, Mohammad Javad Zarif, United States
My last post on how I write formal articles stressed the importance of figures. I thought it might be helpful to expand on that idea. In short, figures are a critical part of the communication process. Good figures separate the well-executed papers from the just good ones. They will reinforce your key points, allow you to write about your results in a more engaging manner, and help you learn more about your model in the process.
Put differently, you need figures in your paper. And the better they are, the better it is for you. These are my thoughts on them.
Why Should I Have Figures?
There are two connected reasons to have figures in your papers: clarity and readability. The majority of formal papers attempt to convince the reader that something that is not obviously true is, in fact, true. We jump through all sorts of hoops to accomplish this. Unfortunately, those hoops are often dense or dull (inclusive or). A picture is worth a thousand words, and replacing a thousand words of abstract mathematics is a win.
Regardless of the mathematics, you want to invite your readers to actually read your manuscript. If someone is skimming through articles, a 10,000 word wall of text is not going to stop them. It also will not stop someone who has read the first five pages and getting bored from closing the window.
But imagine instead one of these readers encounters a figure that shows them something really strange. Someone who was not planning to read your paper might want to learn how the figure came to be. And it might also convince your slipping reader that the ride is worth continuing.
What Should Be Made into a Figure?
My rule of thumb when making figures is to pretend that I am doing an invited talk for the paper I am writing. What do I want to put in the slides to illustrate all my main points? I do not want a slide that says “Proposition 3: The probability of war is nonmonotonic in its costs.” That is boring. I should instead have a plot that illustrates the point. After thinking about all of those slides I would want to make, I will then put almost all of them in the paper itself.
More concretely, I almost always want an equilibrium plot that varies a parameter of interest and shows how the equilibrium changes. These come in two forms. The first is one dimensional. If the narrative you are telling only focuses on one variable, then put that variable on a number line. Add some cutpoints on that number line, and describe the equilibrium behavior associated with it.
Here is an example from my Doubling Down paper:
We are varying the quantity of a CDF evaluated at a particular value. Because it is a CDF, we have bounds on 0 and 1. There are two cutpoints also labeled along the axis that separate the three equilibrium parameter spaces. The top part gives a little context of what is happening in the equilibrium and matches that description to the corresponding proposition in the text. Keep in mind that these are not hard rules about what should be in the figure—what you ultimately put into it depends on what you think is important to communicate with the reader.
The second type figure is two dimensional. These are more complicated to build but are necessary if the narrative is on how large some quantity is related to another. The first step is to put all of the cutpoints in terms of one parameter. This becomes your vertical axis. Your horizontal axis is the other variable of interest. The equilibrium regions of the corresponding figure are now shapes that you can fill in with the critical information.
Here is an example from my Bad-Faith Cooperation paper:
The two key parameters we vary in this figure are the cost and effectiveness of resistance. The labels tell the reader what type of signaling strategy the types adopt for each parameter space and how much resistance the actor chooses within the equilibrium space.
To actually draw two dimensional figures correctly, you need to use realized values of the parameters. It will often take some finagling to get the ideal spacing for each region and to make sure that the each parameter space you want to cover exists for those realized values. As a result, there are usually a lot of moving parts in the final figure you draw. I try to compensate for that by removing any extras that do not absolutely need to be in the figure. This is why the two dimensional figure does not have axis labels for the cutpoints, unlike the one dimensional figure.
Outside of equilibrium plots, you should consider drawing figures for any comparative statics of interest. Any nonmonotonicities or discontinuities always make the cut. Here is an example of that from my Credible Commitment in Covert Affairs paper:
The horizontal axis varies how much trouble an executive gets in if a covert action is exposed. Even if I have lost a reader during the modeling section, there is a good chance that this figure will pull them back in. The executive would seem to be hurt by the potential to get into trouble. The black line on the figure would appear to confirm that. But why does it suddenly go up (red) and then level off (gray)? That is puzzling. I may just have pulled the reader back into the text to find out the answer.
For the most part, the only comparative statics do not receive corresponding figures are basic monotonic relationships, especially if the plot would be just a straight line. Even then, if something strictly increases before becoming flat, I may still want to include that.
How Do I Make Better Looking Figures?
Now that we have established why you should have figures and what is worth figuring, you may want to spend some time making those figure look more attractive. I have two tips here.
First, I strongly recommend TikZ. It integrates seamlessly with TeX, so you can insert math expressions at the proper cut points. It offers precision in what you draw that you cannot obtain from computer-assisted hand drawing. You can even use functions to draw your lines, meaning that you are visualizing exactly what the value is and not some approximation. And it is rendering all of this as a PDF, so your figures will scale nicely with the rest of your document.
The other major recommendation I have is to use color. Oftentimes, adding color will reduce the complexity of the figure, and it also helps make the figure pop out of the document. For equilibrium plots, this means giving each region its own color. Narrating the figure becomes easier, now that you can describe regions by color and not by location.
For estimated quantities, this means giving each value drawn its own color. Actor A’s utility could be black, while Actor B’s utility could be red. If there is only one line to be drawn, then sticking with black and white is fine. Sometimes, though, you will still want to use multiple colors for the same line. This can help distinguish between two regions of the figure as you are narrating it in the text. The utility plot above is an example of that.
The one word of caution I have here is that you are a researcher and probably not a graphic designer. When you start adding a ton of different colors, it is easy to inadvertently create clashing palette. The simple solution to this is to rely on preexisting sets of colors.
These are easy to find online, and universities conveniently give all of the information you need. A simple Google search consisting of the university name + identity (e.g., University of Pittsburgh identity) usually gives you what you need. The key piece of information is the RGB values for the brand colors. You can then define those colors in the preamble of your TeX file (e.g., \definecolor{cardinal}{RGB}{140,21,21}), and use the newly named color in the TikZ commands. I think that Stanford and University of North Carolina are particularly good for these purposes.
One thing to be mindful of is whether the colors are distinguishable in grayscale. Publishers now commonly allow for colored images appear in the online version of articles, but whatever goes to the printer needs to be black and white. Moreover, a peer reviewer may use an office printer to print your color PDF before reading it. Verifying that every color is distinct in grayscale will reduce that reviewer’s frustration.
Suppose you want to write a formal theory paper. Below is the template I use to do this. I do not always follow these rules. But whenever I break them, I usually justify to myself first why it is a good idea to sidestep the norm.
The Introduction
My introductions usually have a set formula:
Of these, I think (5) is the biggest problem I see as a peer reviewer. There are way, way too many papers that will say things along the lines of “increases in income decrease the probability of terrorist attacks” full stop. The intuition explaining the connection will not appear for the first time until page 18 or so. This fundamentally misses the point of doing formal theory. We are not interested in the what. We are interested in the why. Formal theory helps elucidate mechanisms. If you are not elucidating the mechanisms in the introduction, you are not writing an effective paper.
To that point, I find it helpful as a reader (and a reviewer) when this part begins with “The model produces x main results. First, …” Then each subsequent x – 1 paragraphs then explains the other results. This gives a good benchmark to the reader of what to expect in the paper and think about what a model look like that would be good for addressing those issues.
Motivation, Sometimes
I have the most variance in what comes next. Sometimes, it is straight to the model. Other times, I give a deeper explanation for why I am building the model that I am.
An underappreciated aspect of formal theory is that it just an exercise in mapping assumptions to conclusions. As the saying goes “garbage in, garbage out.” If the assumptions you put into a model make little sense, then there is no reason to pay attention to whatever the model outputs. Thus, if readers may view the assumptions your model makes as controversial, this is the time to defend them.
Sometimes, this is unnecessary. For example, if the model takes an existing approach and adds uncertainty, then you probably only need a couple of citations in (3) from the introduction to take care of it. Otherwise, I think through the main critical assumptions from the model. I then begin the second section by listing them. The following paragraphs take each assumption and motivate them. Basically, this is an exercise in going through the existing literature to demonstrate that your assumptions have merit. Key places to draw from are:
Of these, (3) is the most useful and the type I try to emphasize.
There are two important notes to this section. First, it is not a literature review. You are not just rehashing what the literature says about a particular subject. You are motivating assumptions. Everything you write should be geared toward that.
Second, this is a good way to come up with research ideas in the first place. As a general exercise, whenever I read through the literature, I think about what assumptions are out there and whether they appear in the more specific areas I work in. When there is a mismatch, it is worth spending some time to think about whether those alternative assumptions fundamentally alter existing ideas.
The Model
My modeling sections usually follow a basic formula:
The plot part is the thing I see as the easiest way to improve papers. A good rule of thumb is to pretend every paper you are writing is going to be used as a job talk paper. Then think about what slides you would want to present to illustrate the key points. For example, if you had a slide that said “the probability of war increases in the cost of fighting,” you would not want to leave it as just that. You would want the next slide to show a plot with cost on the x-axis and the probability of war on the y-axis. After going through this mental exercise, every visualization of the results should go in the paper.
Empirical Evaluation
This section may or may not exist. Some models require so much space that doing any sort of empirical evaluation is not impossible given the 10,000 word limit you have to aim for to fit most outlets. Otherwise, there are two ways to go here.
Option 1 is to do some sort of qualitative examination. Hein Goemans and I have written about this in Security Studies. If you want to go down this route, you should read that.
The main trap I see when papers take qualitative approach is matching outcome to outcome. For example, the model might predict that poor people commit terrorism, and then the case study talks about how poor people commit terrorism in a certain country.
This misses the point of doing formal theory. As I described above, models map assumptions to conclusions. Case studies should do the same. In other words, I take the three or so assumptions that are key to the model’s mechanism. I then motivate why those assumptions held in the particular case. Only then is the outcome variable worth mentioning. But the key here is to establish that the incentives that the model describes was key to the actors’ reasoning. (Or at least those incentives plausibly drove it. There are many cases where finding a smoking gun would be a ridiculous expectation. If that is the case, then you should make an argument about why it is ridiculous.)
Option 2 is a quantitative examination of a comparative static. Most of this follows the basic quantitative paper template, so there is not much more to say here. The only thing worth adding is that you need a subsection that pivots the comparative static to a hypothesis that you can test. (Comparative statics are true statements. Hypotheses are things that may or may not be true of data.)
Conclusion
I think conclusions are overrated, so I have a simple formula for this:
Posted in Game Theory, Publishing
Tagged article, formal theory, how to, Publishing, writing
Compliance is a central issue in arms control negotiations. Take Iran as an example. The United States has long pitched a better world standing for Iran in exchange for Tehran ending its pursuit of nuclear weapons. President Obama once described such an agreement in the following way:
Iran must comply with UN Security Council resolutions and make clear it is willing to meet its responsibilities as a member of the community of nations. We have offered IRan a clear path toward greater international integration if it lives up to its obligations…. But the Iranian government must now demonstrate through deeds its peaceful intentions…
At first pass, such a trade may seem impossible. The United States has to give concessions to Iran to make nonproliferation look attractive. But nothing stops Iran from accepting those concessions, building nuclear weapons anyway, and then leveraging its atomic threat for all of the corresponding benefits. Worse, if the United States expects this, then it has no incentive to offer any sort of deal in the first place.
I, for one, certainly felt that way when I watched Obama pitched the deal in 2009. In fact, I wrote a book that explores those incentives, which just came out:
Bargaining over the Bomb’s central finding is that, despite appearances to the contrary, those deals work. Countries like Iran do not have an inherent incentive to take those concessions and run with them. This is true even if Iran could build nuclear weapons without the United States noticing until the bombs are finished.
A little bit of formalization helps explain why. All we need are a few parameters to map out the incentives. Suppose that nuclear weapons are useful for coercive leverage, and let p be the percentage of the benefits the would-be proliferator can extract once it has acquired those weapons. Let c > 0 represent the cost of building them. Finally, let 𝛿 > 0 represent how much the would-be proliferator cares about the future.
From this, we can calculate what portion of the benefits the would-be proliferator requires now and for the rest of time to not want to develop nuclear weapons. Let x be that necessary share, so that if a deal is made and sustained, the would-be proliferator receives x for today and 𝛿x for the future, for a total payoff of (1 + 𝛿)x.
The apparent barrier to agreements is that the would-be proliferator can take x for today, pay the cost c, acquire nuclear weapons, and then capture p portion of the benefits in the future. And if it can get away with keeping that x value in the interim, why wouldn’t it?
Well, summing up that payoff for proliferation and comparing it to the payoff for accepting the deal, the potential proliferator prefers to not build if:
(1 + 𝛿)x > x + 𝛿p – k
x > p – k/𝛿
In fact, the would-be proliferator is willing to accept an agreement after all!
Where did intuition fail us? The key to understanding why an agreement works is that proliferation only provides a finite amount of benefits. If the opponent offers the potential proliferator those benefits up front, then proliferating at that point is unprofitable—developing weapons leaves the potential proliferator exactly where it was before, but it must pay the costs of proliferation in the interim.
We can see those incentives in the minimum acceptable offer. The value x must be close to p—in other words, the quantity of concessions given immediately must be close to the benefits the potential proliferator would receive if it built the weapons.
To be more precise, the opposing state can fudge this a little—by k/𝛿, to be exact. This is because, by accepting the deal, the would-be proliferator does not have to pay the cost to build. Note that when the would-be proliferator does not care at all about the future, 𝛿 goes toward 0, and thus the potential proliferator needs less to accept an agreement.
In Bargaining over the Bomb, I develop this model in much greater depth, providing context in how the states calculate the benefits of proliferation, how preventive war fits into this, and whether the opponent would actually want to offer such a deal. But the central finding remains: would-be proliferators are happy to accept agreements. The first half of the book explores some facets of those agreements while the second half explains why bargaining may still fail.
Building this model and writing the book has made me a lot more optimistic about whether negotiations with countries like Iran can succeed. If you share the same skepticism I once did, I would encourage you to read the book and think more about the central incentives at play. I don’t think agreements are universally workable, but they should be a critical part of our policymakers’ tool kits.
Posted in Bargaining, nuclear weapons
My first book with original research just came out. (Amazon even has proof!) This excites me, as you can see from this picture from a couple of weeks ago, when I held it it my hands for the first time:
Part of my elation came from reflecting on just how long I had been working on the project. I thought it might be interesting for younger scholars to get a full perspective, so I am writing out a brief timeline of book-related events here. It might also give a better overview on the origins, thought process, and evolution of a long-form project. There is also going to be a healthy dose of luck. And regardless of utility to others, it’s going to be cathartic for me.
Here goes:
9/25/2009: Yes, we are starting almost ten years ago. I was in my gap year between undergrad and grad school. Applications were not yet due, but I was set on getting into a program and making international relations research into a career.
Globally, Iran was getting bolder with its nuclear program. President Obama, at a G20 summit, issued a warning:
Iran must comply with U.N. Security Council resolutions and make clear it is willing to meet its responsibilities as a member of the community of nations. We have offered Iran a clear path toward greater international integration if it lives up to its obligations, and that offer stands. But the Iranian government must now demonstrate through deeds its peaceful intentions or be held accountable to international standards and international law.
I remember watching Obama make that speech (which YouTube has preserved for posterity) and thinking that such a bargain would not work. Everything I had read at that point about credibility and commitment problems would suggest so. Why wouldn’t Iran simply take the short-term concessions and continue building a weapon anyway? No paper had constructed that exact expectation yet, and so I thought it would be a straightforward project.
Nevertheless, it would have to go on the backburner. I still needed to revise my existing writing sample and do grad applications.
4/2010: By this point, I had accepted an offer from the University of Rochester. I started fiddling around with modeling Obama’s deal and came to an interesting conclusion. It seemed that compliance was not only reasonable, it was rather easy to obtain. All the proposing country had to do was give concessions commensurate with what the potential proliferator would receive if it had nuclear weapons. The potential proliferator could not profit by breaking the agreement, as doing so would barely change what it was receiving but would cost all of the investment in proliferation. Meanwhile, as long as the potential proliferator could keep threatening to build weapons in the future, the proposer would not have incentive to cut the concessions either.
This project was a lot more interesting than I thought it would be!
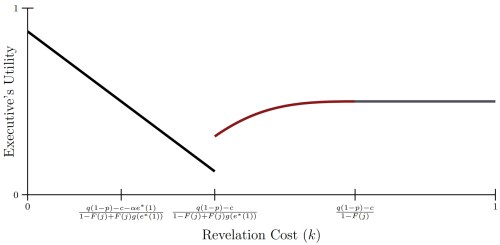
8/8/2010: I moved to Rochester and got serious about trying to formalize the idea. The problem was that I had only taken a quarter of game theory before. So the process was … painful, especially in retrospect. I still have an image of my work from way back when:
I can make out some of what I was trying to do there. It is ugly. But I also think this is useful advice for new students. As a first year grad, you are in a very low stakes environment. Trying to do something and doing it poorly still gets you a foothold for later.
In any case, active progress on this was slow for the next couple of years. I had to take some classes to actually figure out what I was doing.
3/9/2012: I watched the previous night’s episode of The Daily Show for no real reason. In a remarkable stroke of luck, it featured an interview with Trita Parsi, an expert on U.S.-Iranian relations. He made some off-the-cuff remarks about Iran’s concerns of future U.S. preventive action. Fleshing out the logic further gave me the basis of Chapter 6 of my book, with an application to the Soviet Union.
9/2012: I made “The Invisible Fist” my second year paper. At the time, this was the biggest barrier for Rochester graduate students, but the idea from three years earlier got me through it.
The major criticism as I circulated the paper was that the model only explained why states should reach an agreement. And while nonproliferation agreements are fairly commonplace, so too are instances of countries developing nuclear weapons. Trying to simultaneously demonstrate that (1) agreements are credible and (2) other bargaining frictions might make states fail to reach a deal anyway was too much for a single article. I began looking for more explanations for bargaining failure beyond the one I had encountered for the Soviet Union.
5/17/2013: My dissertation committee felt that I had found enough other explanations, as I passed my prospectus defense. This was the first time I produced an outline that (more or less) matches what the book would ultimately look like.
12/2014: International Interactions R&R’d an article version of Chapter 6. It would later be published there. Tangible progress!
5/2015: Reading through the quantitative empirics of my book, Brad Smith suggested a better way to estimate nuclear proficiency. This eventually became our 𝜈-CLEAR paper. I would later replace the other measures of nuclear proficiency in the book with 𝜈.
6/10/2015: After two years of grinding through lots of math and writing, I defended my dissertation. Hooray, I became a doctor!
7/14/2015: The Joint Comprehensive Plan of Action—a.k.a. the Iran Deal—is announced. This was could not have been timed any better. Chapter 7 of my book was a theory without a case, only a roundabout discussion of the Iraq War. But the JCPOA nailed everything that the chapter’s theory predicted. I began revising that chapter.
8/2015: I began a postdoc at Stanford. My intention was to use the year to get the dissertation into a book manuscript and talk to publishers. But after six years of thinking about nuclear negotiations and not much else, I was really burned out. I still received excellent feedback on the project during the postdoc, but I set aside almost all of it. The year was productive for me overall, just not on the one dimension I had intended.
10/2015: The JCPOA went into effect. With nuclear negotiations all over the news, I hit the job market at exactly the right time.
7/2016: I moved to Pittsburgh. Remember that Obama speech in front of the G20? In what is a remarkable coincidence that bookends my journey, that summit was just a couple of miles away from where my office is now.
1/2017: I was still burned out. This became a moment of reflection, where I realized that 20 months had passed without making any progress on the manuscript. I convinced myself that if I didn’t get moving, the thing would hang over my head forever and not provide me any value toward a tenure case. So I cracked down and got to work.
3/2017: I sent an email to an editor at Cambridge. He quickly replied, and we set up a meeting at MPSA. Once in Chicago, he liked my pitch and asked to see a draft when I was ready.
5/22/2017: After making some final changes to the manuscript, I sent off a proposal, the introductory chapter, and the main theory chapter to Cambridge.
6/6/2017: My editor wrote back asking for the full manuscript to look over. I did so the next day. One day later, I saw an email notification on my phone that he had responded. I panicked—there is no way that a one-day response could be good news, right? But it was!
You may notice a theme developing here: my editor was fast.
9/6/2017: After three months, the reviewers come back with an R&R. Hooray!
Having published a few articles beforehand, the R&R process was not new to me. But it is an order of magnitude more complicated for book manuscripts. Article reviews are rarely more than a couple of pages. In contrast, I had twelve pages of comments to wade through for the book. This was daunting: a mountain of work and a lengthy road before any of it actually makes noticeable progress to any outside observer. After having gone through almost two years of burn out on the project, this had me slightly worried.
9/12/2017: I developed a solution to the problem that would work. The key for me to maintain focus and appreciate progress was to create a loooooong list of all the practical steps I had to take in revising the manuscript. By the end, I had a catalog of 70 things to do. I put that number on my whiteboard:
I dedicated at least a couple of hours every day to working on the book. Whenever I finished an item, I would go to the whiteboard and knock the number down by one. This gave me some tangible sense of progress even when the work ahead still seemed enormous. It also kept me focused on this project and resist the temptation to work on lower-priority projects that I could finish sooner.
11/28/2017: I sent the revised manuscript back.
1/28/2018: The remaining referee cleared the book. All the hard steps were over!
3/28/2019: I held the real thing in my hand for the first time.
So almost ten years later, I am all done with the project. I cannot describe how satisfying it was to move the book’s computer documents out of the active folder and into the archived folder. I can now finally put all of my effort into the other projects that have been pushed to the sidelines.
But with all of that said, ten years feels like a bargain. Some of that time was pure circumstances: I had to actually learn how to be a political scientist for a good portion of it. I was also an okay writer at the beginning of this, but now I feel that I have a much better grasp of how to communicate ideas.
Nevertheless, some portion of it was my own fault. I could have not put the project on the back burner for more than a year. I suppose if that was the price I had to pay to maintain my own sanity and happiness (and not work on something I was not into at the time), it was a deal well-worth taking.
I was also really, really fortunate with the review process. The first editor I spoke to was receptive of the project, and the reviewers I pulled liked it. Had that not been the case, it is easy to see how a ten year project could have turned into a twelve or thirteen year project. While I hope that future book projects will not last as long, I doubt this part will be as simple the next time around.
In any case, it feels great to finally be done!
Posted in nuclear weapons, Political Science, Publishing
Defense Secretary James Mattis has called for relief to North Korea to only come after it takes “irreversible steps to denuclearization.”
Let’s set aside the question of whether this will happen. It probably won’t. The United States cannot credibly commit to not invade a nuclear-free North Korea under the right circumstances, and so North Korea will keep its deterrent to hedge against that. And even if that credible commitment were not a concern, the ability to build nuclear weapons drives concessions. North Korea would not agree to “irreversible” denuclearization if only to maintain its ability to leverage the threat to build again.
Instead, let’s focus on a more interesting question: can you make nuclear proliferation irreversible? This is difficult to answer because you first need to somehow quantify a state’s nuclear proficiency. One cannot observe proficiency directly, only behaviors consistent with low or high proficiency.
Fortunately, Brad Smith and I have developed a measure of this. ν-CLEAR takes observable nuclear behaviors and uses that information to estimate a country’s nuclear proficiency. We are currently working on a massively expanded version of the data, and one of our findings speaks to the situation with North Korea.
Consider the role of uranium enrichment and reprocessing on nuclear proliferation. This is a critical step toward actually building a nuclear weapon. Bombs need fuel, and to have fuel you need to either enrich uranium or reprocess plutonium from spent uranium. The Yongbyon Nuclear Scientific Research Center has such a facility. Any deal like what the Trump administration hopes for would involve shutting this down.
However, shutting down a facility does not necessarily make nuclear proliferation irreversible. Unless actually operating an enrichment or reprocessing facility radically shifts a country’s nuclear proficiency, North Korea could just construct a new one.
Our data and a little bit of historical knowledge can help us understand the relationship between fuel facilities and nuclear proficiency. Argentina operated its Pilcaniyeu Enrichment Facility until 1994. Let’s look at a timeline of Argentina’s nuclear proficiency before and after. Larger values mean greater proficiency:
Closing the facility had an effect. But it’s marginal. Let’s zoom in on 1994:
Argentina’s proficiency score definitely drops. However, operating the facility is only of marginal importance.
What is going on here? The issue is that having a facility and knowing how to create a facility are two different things. A country that builds fuel fabrication centers also has the nuclear capacity to engage in other nuclear activities. Our estimation procedure incorporates those factors into a state’s overall score. When a state shuts down those facilities, the procedure penalizes that state’s score. But it also recognizes the state’s other nuclear activities as evidence of its ability to rebuild a facility if it wanted to. As a result, ν does not believe that operation of the facility tells us much about what Argentina can or cannot do.
Bringing this back to North Korea, it is unlikely that any sort of divestment will irreversibly cancel North Korea’s nuclear weapons program. For these purposes, knowing how to do things is more important than actually doing them. As long as North Korean nuclear scientists retain their knowledge, Peongyang will always be able to restart the program.
As a final note, to be clear, I am not suggesting that the U.S. should ignore the importance of the Yongbyon Nuclear Scientific Research Center. When Donald Trump meets Kim Jong-un, it should be an important topic of discussion. The ν measure only captures what states can do. It does not care much about time delays. Shuttering Yongbyon would probably not reduce North Korea’s ability to develop more fuel. But it would increase the time necessary to do that because North Korea would have to rebuild the facility. And that’s a goal worth obtaining.
As more returns come in from California, it looks like Trump is going to lose the popular vote despite having secured a majority of electoral votes. In the coming days, if the 2000 election was any indication, I suspect we will see Democrats arguing that this somehow makes Clinton the “rightful” president and that Trump wouldn’t be president if we had a “more sensible” electoral system.
These arguments are silly: the popular vote tells us virtually nothing about what an election would have looked like if the popular vote mattered.
The basic idea is that elections are strategic; campaigns adopt particular tactics given the rules of the game. Consequently, we cannot judge whether Clinton would have won in a popular vote contest given the results of an electoral vote contest.
Here’s an analogy to make the idea more concrete. Baseball games are decided by runs. Teams strategize accordingly, sometimes sacrificing outs to get a man across the plate. This occasionally results in games where the winner gets fewer hits than the loser.
If you change the rules of the game, you change the strategic incentives. Award wins based on hits, and suddenly those sacrifice strategies would never happen. As such, we can’t retroactively award wins based on hits for games where the teams were strategizing for runs.
Similarly, if only the popular vote mattered, campaign incentives change. Candidates choose which policies they support based on the pivotal voter in the election. With an electoral vote, this is the median of the median voters of each state. With a popular vote, this is simply the median voter of the country.
Individual level incentives change as well. With an electoral vote, people in California have fewer incentives to go to the polls than someone in Pennsylvania; the result in California is a foregone conclusion, whereas the result in Pennsylvania is in doubt and could sway the electoral college. With a popular vote, each individual’s incentives are identical.
Thus, we don’t know how the election would have turned out under a different electoral system. Given the high concentrations of Latinos in otherwise uncompetitive states (California, Texas), it’s extremely unlikely that Trump would been as ardent in his anti-immigration policy if the popular vote mattered. And that alone means that we can’t use Tuesday’s returns to judge how a popular vote would have played out.
Bottom line: Trump won with the system we are playing with, and that’s all that matters.
Posted in Institutions, Political Science
According to many popular theories of war, the answer is yes. In fact, this is the textbook relationship for standard stories about why states would do well to pursue increased trade ties, alliances, and nuclear weapons. (I am guilty here, too.)
It is easy to understand why this is the conventional wisdom. Consider the bargaining model of war. In the standard set-up, one side expects to receive p portion of the good in dispute, while the other receives 1-p. But because war is costly, both sides are willing to take less than their expected share to avoid conflict. This gives rise to the famous bargaining range:
Notice that when you increase the costs of war for both sides, the bargaining range grows bigger:
Thus, in theory, the reason that increasing the costs of conflict decreases the probability of war is because it makes the set of mutually preferable alternatives larger. In turn, it should be easier to identify one such settlement. Even if no one is being strategic, if you randomly throw a dart on the line, additional costs makes you more likely to hit the range.
Nevertheless, history often yields international crises that run counter to this logic like trade ties before World War I. Intuition based on some formalization is not the same as solving for equilibrium strategies and taking comparative statics. Further, while it is true that increasing the costs of conflict decrease the probability of war for most mechanisms, this is not a universal law.
Such is the topic of a new working paper by Iris Malone and myself. In it, we show that when one state is uncertain about its opponent’s resolve, increasing the costs of war can also increase the probability of war.
The intuition comes from the risk-return tradeoff. If I do not know what your bottom line is, I can take one of two approaches to negotiations.
First, I can make a small offer that only an unresolved type will accept. This works great for me when you are an unresolved type because I capture a large share of the stakes. But if also backfires against a resolved type—they fight, leading to inefficient costs of war.
Second, I can make a large offer that all types will accept. The benefit here is that I assuredly avoid paying the costs of war. The downside is that I am essentially leaving money on the table for the unresolved type.
Many factors determine which is the superior option—the relative likelihoods of each type, my risk propensity, and my costs of war, for example. But one under-appreciated determinant is the relative difference between the resolved type’s reservation value (the minimum it is willing to accept) and the unresolved type’s.
Consider the left side of the above figure. Here, the difference between the reservation values of the resolved and unresolved types is fairly small. Thus, if I make the risky offer that only the unresolved type is willing to accept (the underlined x), I’m only stealing slightly more if I made the safe offer that both types are willing to accept (the bar x). Gambling is not particularly attractive in this case, since I am risking my own costs of war to attempt to take a only a tiny additional amount of the pie.
Now consider the right side of the figure. Here, the difference in types is much greater. Thus, gambling looks comparatively more attractive this time around.
But note that increasing the military/opportunity costs of war has this precise effect of increasing the gap in the types’ reservation values. This is because unresolved types—by definition—view incremental increases to the military/opportunity costs of war as larger than the resolved type. As a result, increasing the costs of conflict can increase the probability of war.
What’s going on here? The core of the problem is that inflating costs simultaneously exacerbates the information problem that the proposer faces. This is because the proposer faces no uncertainty whatsoever when the types have identical reservation values. But increasing costs simultaneously increases the bandwidth of the proposer’s uncertainty. Thus, while increasing costs ought to have a pacifying effect, the countervailing increased uncertainty can sometimes predominate.
The good news for proponents of economic interdependence theory and mutually assured destruction is that this is only a short-term effect. In the long term, the probability of war eventually goes down. This is because sufficiently high costs of war makes each type willing to accept an offer of 0, at which point the proposer will offer an amount that both types assuredly accept.
The above figure illustrates this non-monotonic effect, with the x-axis representing the relative influence of the new costs of war as compared to the old. Note that this has important implications for both economic interdependence and nuclear weapons research. Just because two groups are trading with each other at record levels (say, on the eve of World War I) does not mean that the probability of war will go down. In fact, the parameters for which war occurs with positive probability may increase if the new costs are sufficiently low compared to the already existing costs.
Meanwhile, the figure also shows that nuclear weapons might not have a pacifying effect in the short-run. While the potential damage of 1000 nuclear weapons may push the effect into the guaranteed peace region on the right, the short-run effect of a handful of nuclear weapons might increase the circumstances under which war occurs. This is particularly concerning when thinking about a country like North Korea, which only has a handful of nuclear weapons currently.
As a further caveat, the increased costs only cause more war when the ratio between the receiver’s new costs and the proposer’s costs is sufficiently great compared to that same ratio of the old costs. This is because if the proposer faces massively increased costs compared to its baseline risk-return tradeoff, it is less likely to pursue the risky option even if there is a larger difference between the two types’ reservation values.
Fortunately, this caveat gives a nice comparative static to work with. In the paper, we investigate relations between India and China from 1949 up through the start of the 1962 Sino-Indian War. Interestingly, we show that military tensions boiled over just as trade technologies were increasing their costs for fighting; cooler heads prevailed once again in the 1980s and beyond as potential trade grew to unprecedented levels. Uncertainty over resolve played a big role here, with Indian leadership (falsely) believing that China would back down rather than risk disrupting their trade relationship. We further identify that the critical ratio discussed above held—that is, the lost trade—evenly impacted the two countries, while the status quo costs of war were much smaller for China due to their massive (10:1 in personnel alone!) military advantage.
Again, you can view the paper here. Please send me an email if you have some comments!
Abstract. International relations bargaining theory predicts that increasing the costs of war makes conflict less likely, but some crises emerge after the potential costs of conflict have increased. Why? We show that a non-monotonic relationship exists between the costs of conflict and the probability of war when there is uncertainty about resolve. Under these conditions, increasing the costs of an uninformed party’s opponent has a second-order effect of exacerbating informational asymmetries. We derive precise conditions under which fighting can occur more frequently and empirically showcase the model’s implications through a case study of Sino-Indian relations from 1949 to 2007. As the model predicts, we show that the 1962 Sino-Indian war occurred after a major trade agreement went into effect because uncertainty over Chinese resolve led India to issue aggressive screening offers over a border dispute and gamble on the risk of conflict.
Posted in Bargaining, nuclear weapons, Political Science, War
Tagged Barga, incomplete information, nuclear weapons, Political Science, uncertainty, war
From Appointing Extremists, by Michael Bailey and Matthew Spitzer:
Given their long tenure and broad powers, Supreme Court Justices are among the most powerful actors in American politics. The nomination process is hard to predict and nominee characteristics are often chalked up to idiosyncratic features of each appointment. In this paper, we present a nomination and confirmation game that highlights…important features of the nomination process that have received little emphasis in the formal literature . . . . [U]ncertainty about justice preferences can lead a President to prefer a nominee with preferences more extreme than his preferences.
Wait, what? WHAT!? That cannot possibly be right. Someone with your ideal point can always mimic what you would want them to do. An extremist, on the other hand, might try to impose a policy further away from your optimal outcome.
But Bailey and Spitzer will have you convinced within a few pages. I will try to get the logic down to two pictures, inspired by the figures from their paper. Imagine the Supreme Court consists of just three justices. One has retired, leaving two justices with ideal points J_1 and J_2. You are the president, and you have ideal point P with standard single-peaked preferences. You can pick a nominee with any expected ideological positioning. Call that position N. Due to uncertainty, though, the actual realization of that justice’s ideal point is distributed uniformly on the interval [N – u, N + u]. Also, let’s pretend that the Senate doesn’t exist, because a potential veto is completely irrelevant to the point.
Here are two options. First, you could nominate someone on top of his ideal point in expectation:
Or you could nominate someone further to the right in expectation:
The first one is always better, right? After all, the nominee will be a lot closer to you on average.
Not so fast. Think about the logic of the median voter. If you nominate the more extreme justice (N’), you guarantee that J_2 will be the median voter on all future cases. If you nominate the justice you expect to match your ideological position, you will often get J_2 as the median voter. But sometimes your nominee will actually fall to the left of J_2. And when that’s the case, your nominee becomes the median voter at a position less attractive than J_2. Thus, to hedge against this circumstance, you should nominate a justice who is more extreme (on average) than you are. Very nice!
Obviously, this was a simple example. Nevertheless, the incentive to nominate someone more extreme still influences the president under a wide variety of circumstances, whether he has a Senate to contend with or he has to worry about future nominations. Bailey and Spitzer cover a lot of these concerns toward the end of their manuscript.
I like this paper a lot. Part of why it appeals to me is that they relax the assumption that ideal points are common knowledge. This is certainly a useful assumption to make for a lot of models. For whatever reason, though, both the American politics and IR literatures have almost made this certainty axiomatic. Some of my recent work—on judicial nominees with Maya Sen and crisis bargaining (parts one and two) with Peter Bils—has relaxed this and found interesting results. Adding Bailey and Spitzer to the mix, it appears that there might be a lot of room to grow here.
According to the theory of outbidding, violent non-state actors have incentive to “advertise” their “services” through violence to capture a larger share of their audience’s support and resources. A natural conclusion drawn from this is that violence increases as the number of groups increases; the greater competition forces these groups to work harder to gain traction in their communities.
While this literature is large and growing, empirical support for a connection between violence and the number of competing groups is mixed. Some large-n studies find that violence positively correlates with the number of groups. Some don’t. What explains this discrepancy?
In a new working paper, I argue that a countervailing deterrence effect helps make sense of the mixed results. At present, outbidding theory only focuses on the competition between groups; it ignores the actions of the target of the violence. Nevertheless, the demands that a target imposes on an affected population influence recruitment rates, and groups have greater incentive to invest in competition when there is a larger pool of money to compete for. Thus, if a target observes a large number of groups and fears that competition will lead to massive violence, it may wish to withdraw from the problem area. This quashes the supply of recruits and reduces competition. In turn, a large number of groups can have a deterrent effect and possibly lead to less violence.
However, it is unclear whether the deterrent effect or the competition effect predominates, so I model the interaction to look for answers. As it turns out, whether more groups implies more violence depends on a seemingly irrelevant characteristic: the function that maps encroachments from the target to civilian support for resistance groups.
Naturally, this function should be increasing. That is, the more the target reduces civil liberties, captures additional territory, or expands its military into foreign lands, the more the effected population would want to support organized resistance. But the rate at which it increases could vary from case to case. Do the initial encroachments lead to a sharp increases in volunteer rates that slowly taper off? Then the function is concave, like the red line in the figure below. Or do initial encroachments lead to marginal increases at first but larger increases at later demands? Then the function is convex, like the black line in the figure.
Surprisingly, the anticipated relationship between violence and the number of groups only holds when the function is convex (black line). The intuition is exactly as the current literature understands outbidding, so I will not explain it any further.
The anticipated effect disappears when the function is concave (red line), though. The explanation is a bit more involved but makes perfect sense in retrospect. Imagine for the moment that the target state wanted to capture a small portion of the good under these concave conditions. This is going to spark a sharp marginal increase in the amount of violence it faces. Thus, if it is worth taking the first bit (and suffering a lot of violence), it is worth taking the entire policy under dispute (and suffering only marginally more violence as a result).
So when the function is concave, the target’s optimization problem is a simple binary choice between taking nothing and taking everything. But recall that violence is increasing in the number of groups. Consequently, with more groups, taking the whole lot looks less attractive. In turn, when the number of groups is low enough, the target takes everything; when that number is high enough, it takes nothing.
Observed violence as a function of the number of competing organizations. The red dots track violence when the function is concave, with black for convex.
As the above figure illustrates, this leads to a nonmonotonic relationship between the number of groups and violence. Below that critical number of groups, violence increases as the number of groups increases. This is because the target is still taking the entire policy under dispute and the additional competition is producing increasingly more violence. But after that critical number, violence drops off because there is no civilian support for the groups to compete for.
The remainder of the paper discusses the empirical implications of the model. The key takeaway here is that we need some way to measure these supply curves to obtain useful large-n estimates of the effect of the number of groups. There is no simple fix here, though foreign interventions are seemingly more likely to fit the concave (red) case.
Again, the paper is here. If you have any comments, please send me an email!
Abstract. The theory of outbidding states that terrorist, insurgent, and rebel groups use violence to capture a greater share of their audience’s resources. I argue that opponents of these groups should endogenously anticipate this dynamic, which potentially alters their aims. Although a seemingly obvious implication of outbidding is that violence increases as the number of groups (and thus competition) increases, I show that this may or may not hold once we factor in the opponent’s decision. This is because the target states—fearing group competition—might endogenously reduce their demands. The results help explain empirical inconsistencies regarding outbidding. Using comparative statics from the model, I then discuss the challenges to making valid inferences regarding outbidding.
Posted in Political Violence, Terrorism
Tagged outbidding, Political Violence, Terrorism
William Spaniel 